Bone Collector

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 65099    Accepted Submission(s): 27122

Problem Description

Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave …

The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?

 

 

Input

The first line contain a integer T , the number of cases.

Followed by T cases , each case three lines , the first line contain two integer N , V, (N <= 1000 , V <= 1000 )representing the number of bones and the volume of his bag. And the second line contain N integers representing the value of each bone. The third line contain N integers representing the volume of each bone.

 

 

Output

One integer per line representing the maximum of the total value (this number will be less than 2

³¹).

 

 

Sample Input

1 5 10 1 2 3 4 5 5 4 3 2 1

 

 

Sample Output

14

 

题目大意：有一个骨头收集者，他有一个容量为V的包，他要收集N根骨头，每根骨头拥有它的价值Valu和占用体积Vol，求最优解。

 

这是个简单的01背包问题，核心算法就是：F[i,v] = max{F[i − 1,v],F[i − 1,v − C i ] + W i } 具体的解释请看我的另一片博文：http://www.cnblogs.com/William-xh/p/7305877.html

 

主要就是还是要进行判断，如果背包放得下的话，那就是要看我放还是不放；如果是放不下的话，那就是不放。

 

这题我是用二维数组解的，一位数组那个代码还没有研究过，就也还没写过。之后要是写的话就码上来。

附上代码：

#include 
      
       #include
       
        #include 
        
         #include
         
          #include
          
           #include
           
          
         
        
       
      

 

然后在此进行一位数组的解释，这边有一个讲的还是比较清楚的：http://blog.csdn.net/qq_32036091/article/details/51301912

一维数组优化

且说小Ho搞清楚了计算方法，正在埋头苦写代码，在一旁看他写代码的小Hi是在看不下去了，决定再指点指点小Ho：“小Ho啊！”

“怎么了？”小Ho眼睛盯着屏幕，望都没望小Hi一眼。

“你现在是不是需要开一个N * M大小的二维数组best，来记录求解出的best值呀？”

小Ho终于有了点反应，抬起头来说道：“是啊，怎么了？“

“我有办法不用开这么大空间哦~”小Hi笑嘻嘻道：”可我就是不告诉你！”

“诶，别这样，我请你吃雪糕！”小Ho一听就急了，连忙许下了报酬。

“开玩笑啦~”小Hi也是随便逗了逗乐子就没继续：“你想想，在i已经是10以上的时候，best(5, j)这样的值还有用么？”

“没有用了……你是说，我并不需要在内存中存下来所有的best(i, j)，没有用了的值都可以不进行保存……也就是说，实际上只要开一个2*M大小的数组就可以了，然后像这样的方式进行来回的计算，是不是就可以了？”

“是的呢！但是还可以更少哦~让我来写这个程序的话，我只需要开一个M大小的一维数组就可以了”小Hi自信的说道：“你想想，如果我按照j从M到1的顺序，也就是跟之前相反的顺序来进行计算的话。另外根据我们的状态转移方程，可以显然得出如果状态(iA, jA)依赖于状态(iB, jB)，那么肯定有iA = iB+1, jA>=jB。所以不难得出一个结论：我在计算best(i, j)的时候，因为best(i, j+1..M)这些状态已经被计算过了，所以意味着best(i - 1, k)，k=j..M这些值都没有用了——所有依赖于他们的值都已经计算完了。于是它们原有的存储空间都可以用来存储别的东西，所以我不仿直接就将best(i, j)的值存在best(i-1, j)原有的位置上，就像这样。”

“原来还可以这样！这样一处理，不仅空间复杂度小了很多，代码也很好看了呢！”小Ho开心道。

“那你还不去写？”

然后，我在这边附一张自己的演示图：

 

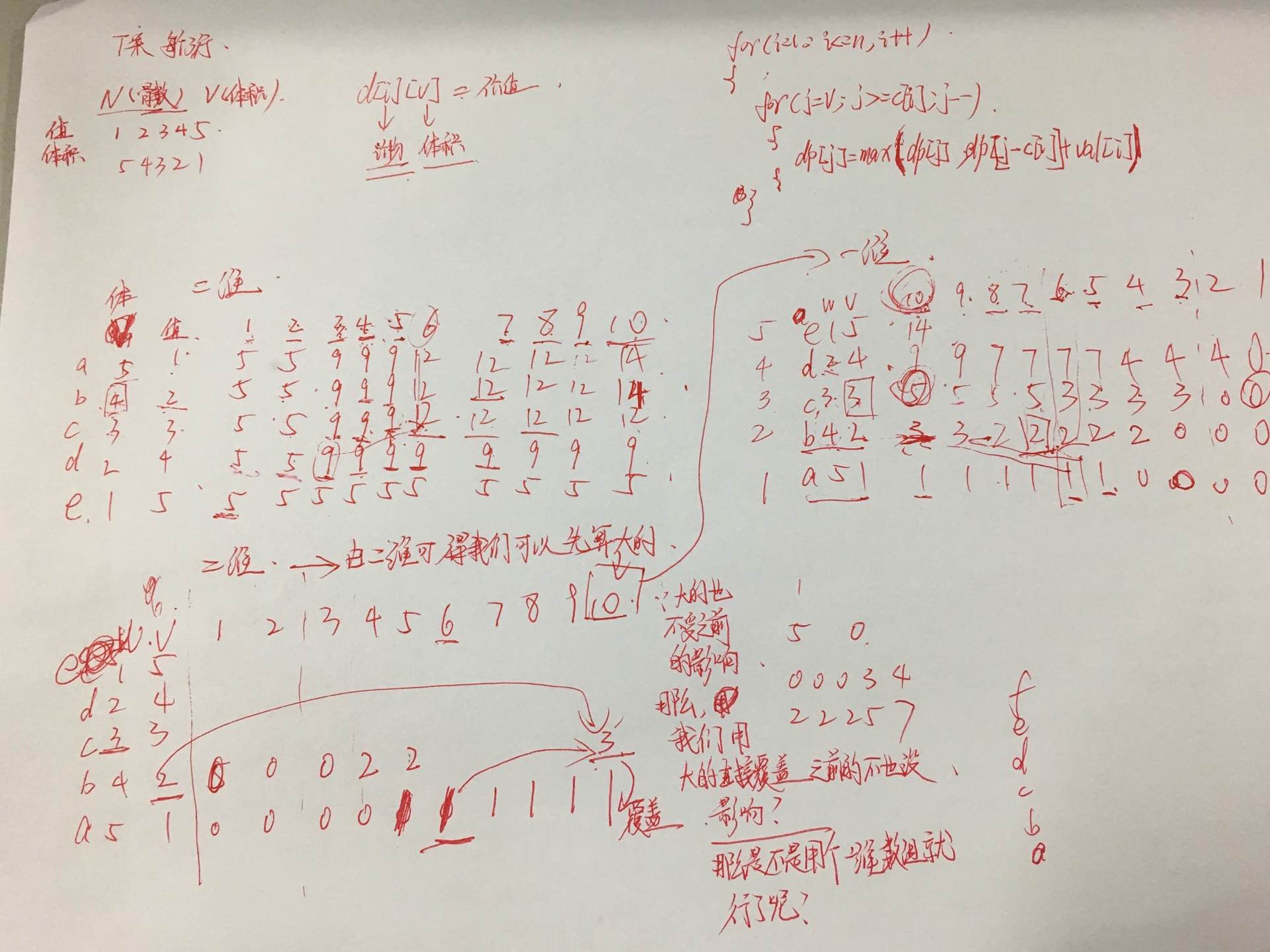
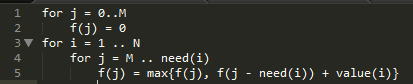
然后，根据你在纸上换算的过程，你可以得到一个核心算法：dp[j]=max(dp[j],dp[j-vol[i]]+value[i]);

其实一维数组的核心就在于：1.从大到小进行计算   2.对之前的数据进行覆盖。

然后附上代码：

#include 
       
        #include
        
         #include 
         
          #include
          
           #include
           
            #include